Catetos a,b e hipotenusa
Fórmula para hallar C
Imagen
Vídeo
Fórmula para hallar B
Fórmula para hallar A
PROBLEMAS RESUELTOS
Problema 1
Calcular la altura que podemos alcanzar con una escalera de 3 metros apoyada sobre la pared si la parte inferior la situamos a 70 centímetros de ésta.
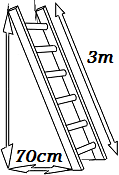
Resolución
Hay que tener en cuenta que las unidades de medida no son las mismas. Podemos escribirlas todas en metros, así que
70 cm = 7 dm = 0.7 m
El triángulo que tenemos es
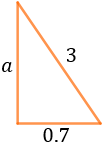
La altura es uno de los catetos. Aplicamos el teorema de Pitágoras para calcularla:
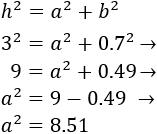
Por tanto,
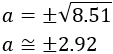
Pero como es la altura, debe ser positiva. Por tanto, la altura será, aproximadamente
Problema 2
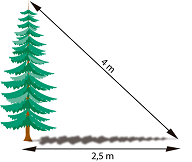
Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
Resolución
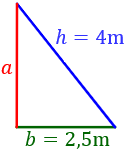
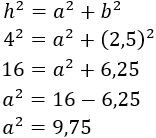
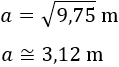
Resolución
Imaginamos un triángulo rectángulo de modo que
- su base, , es la sombra del árbol,
- su altura, , es la altura del árbol y
- su hipotenusa, , es la distancia desde el árbol al extremo de la sombra.

Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, :
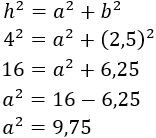
Finalmente, hacemos la raíz cuadrada:
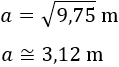
Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.
Problema 3
Un parque de diversiones quiere construir una nueva atracción que consiste en una tirolesa que parte desde la base superior de una columna con forma cilíndrica. Si el radio de la columna es metros y el área de su lateral es de 120 metros cuadrados, calcular la longitud del cable de la tirolesa para que alcance el suelo a 40 metros de distancia de la columna.
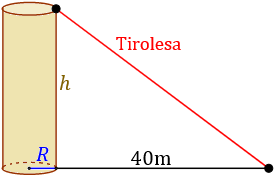
Resolución
Tenemos un triángulo rectángulo de base 40m cuya hipotenusa coincide con la tirolesa. La altura de la columna, , la podemos calcular a partir de su área lateral y su radio, .
El área lateral del cilindro es la del rectángulo de altura y cuya base es el diámetro de la base del cilindro, es decir, dos veces el radio.
Por tanto, el área del lateral de la columna es
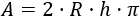
Sustituimos el área () y el radio () y resolvemos la ecuación:
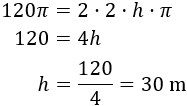
Luego la altura de la columna es de 30 metros.
Finalmente, calculamos la hipotenusa aplicando el teorema de Pitágoras:
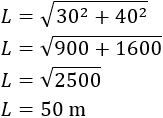
Nota: hemos llamado a la hipotenusa para no confundirla con la altura de la columna.
El cable de la tirolesa debe medir 50 metros de longitud.
PROBLEMAS A RESOLVER
Ejercicio 1
Un clavadista está entrenando en una piscina con una plataforma. Cuando realiza el salto, cae a una distancia de 1 metro de la plataforma sumergiéndose 2,4 metros bajo el agua. Para salir a la superficie, bucea hasta el final de la piscina siguiendo una línea transversal de 8,8 metros de longitud.
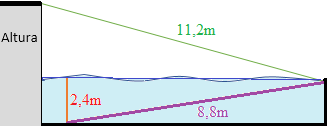
Si la longitud desde la parte superior de la plataforma al lugar en donde emerge del agua es de 11,2 metros, ¿cuál es la altura de la plataforma (desde el nivel del agua)?
Ejercicio 2

Ejercicio 3
Ejercicio 2
Una palmera de 17 metros de altura se encuentra sujeta por dos cables de 21m y 25m respectivamente. En la figura se pide calcular la distancia AB.

Ejercicio 3
Calcular la altura de un triángulo equilátero, sabiendo que su lado es 4cm.
Ejercicio 4
En la figura se muestra una escalera que está apoyada hacía una pared. Se pide calcular el perímetro del triángulo rectángulo que se forma.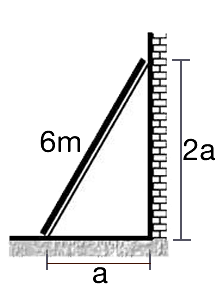




No hay comentarios:
Publicar un comentario